Explore Simple Game Algorithms With Color Walk: Part 6

What's next with exploring different game algorithms using the simple game Color Walk? We've come a long way so far with building out the game's interface to support looking at different algorithms, looking at trivial round-robin and random algorithms, and designing a greedy algorithm that picked each move based on the most blocks removed. The last post showed how far we could push the greedy algorithm to look ahead and try to pick a better move that would result in more blocks removed up to five moves ahead, but even after improving the data structure for the board, we hit diminishing returns in looking more moves ahead. It's time to expand our search for algorithms by looking at other heuristics we can use to pick the best move. The greedy algorithm used a heuristic of "the most blocks removed" for any given move, but there are others that we can use.

Expand the Perimeter

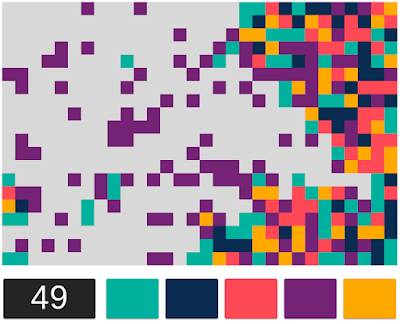
The greedy algorithm's heuristic can be considered an area heuristic. Each block is one unit of area, and removing blocks increases the amount of empty area on the board. The greedy algorithm tries to maximize that empty area on every move (or eventually when looking ahead to future moves). Instead of maximizing area, we could have it try to maximize something else, and the most obvious thing after area to maximize is the perimeter. Take the following picture of the start of a game, for example:

If we look at dark blue as the next move, then we would expand the area of the empty space by four blocks. Instead of the area, we could look at the perimeter of these blocks and see that by removing them, we have exposed seven new perimeter lengths of empty space. A "perimeter length" is simply an edge of a block, for the purposes of counting. A removed block can add up to three lengths to the new perimeter, such as that lone pink block next to the empty space in the picture above. Adding that pink block's perimeter to the 'L' shaped pink cluster below results in nine new perimeter lengths if pink is chosen on the next move, and that would be the move to chose if we were maximizing perimeter.

To count the perimeter, we want to make sure we're not counting edges along the empty space because those edges don't matter. They won't be a part of the new perimeter if the corresponding blocks were removed, but rather, they would be inside the expanded empty space. To assess how much the perimeter has expanded, we want to only count edges that would still exist once the blocks were removed. Now that we have an idea of what this new heuristic should do, let's look at how to implement it.

You generally have two choices for how to proceed when adding a feature: bottom-up or top-down. We can start either from the bottom with adding the new heuristic count metric, or at the top with adding the new max-perimeter algorithm choice to the list of options. Let's start at the bottom and build up this time. First, we'll add new functions called areaCount() and perimeterCount() to the general functions available outside any object:

  function areaCount() {
    return _.filter(blocks, function (block) {
      return (0 !== block.marked);
    }).length;
  }

  function perimeterCount() {
    var count _.reduce(blocks, function (accum, block) {
      if (block.marked === 0) return accum;
      return accum + _.filter(block.getNeighbors(), function (neighbor) {
        return blocks[neighbor].marked === 0 && !blocks[neighbor].isDead;
      }).length;
    }, 0);

    if (count === 0) return areaCount();
    return count;
  }

The areaCount() function does the work of counting marked blocks from the original greedy algorithm heuristic, and it's just a packaging up of code we've already seen into a function. The perimeterCount() function does all of the dirty work of counting perimeter edges for the new heuristic. The outer _.reduce() operation scans through all blocks accumulating edge counts. For each block, if the block isn't marked, we just ignore it and return the accumulator unchanged. For any block that is marked (meaning, the block is being considered for removal), we want to _.filter() all of it's neighbors and count the ones that are not marked and not dead. That combination identifies those blocks that are not currently being considered for removal or part of the empty space. Any such block that's a neighbor of a marked block will be on an edge that makes up the new perimeter, so we count it. It should be clear from this function that it will work in general whether we are looking one move ahead or more, so we can use this heuristic in a look-ahead version of max-perimeter, too.

Notice that the perimeter case will fall back on areaCount() if there is no new perimeter count found. This situation happens near the end of a game, when all of the blocks that are left on the board are disjoint. If we didn't fall back on areaCount(), the algorithm would get stuck in an infinite loop, picking the first color indefinitely since all of the colors result in zero new perimeter count. When that happens, we want to go ahead and pick the color that removes the most blocks to finish up the game.

If you also noticed the call to block.getNeighbors() and wondered where that came from, the function getNeighbors() was moved from Cluster to Block, because it definitely makes more sense to have it in the Block:

  function Block(x, y, color, i, isDead) {
    // ...

    this.getNeighbors = function() {
      var neighbors = [];
      var i = this.position;
      if (i % grid_length > 0) {
        neighbors.push(i - 1);
      }
      if (i % grid_length + 1 < grid_length) {
        neighbors.push(i + 1);
      }
      if (i - grid_length > 0) {
        neighbors.push(i - grid_length);
      }
      if (i + grid_length + 1 < grid_length * grid_height) {
        neighbors.push(i + grid_length);
      }

      return neighbors;
    };
  }

Naturally, the other calls to getNeighbors() need to be changed to block.getNeighbors() as well. Now this function can be called from outside of Cluster so we can use it in the perimeterCount() metric to count perimeter edges.

What we're actually doing here is adding a new option to the greedy algorithm instead of creating an entirely new algorithm. To use this new perimeterCount() function, we want to call it at the end of Control.checkGameBoard() where we were counting the removed blocks before:

    this.checkGameBoard = function(check_move, metric) {
      _.each(blocks, function (block) {
        if (block.marked >= check_move) {
          block.marked = 0;
        }
      });

      blocks[0].cluster.markNeighbors(this.color, check_move);

      return metric();
    }

Here we changed the code that counts marked blocks to instead call a function that describes which metric we want to use when assessing the marked blocks. Currently those functions can be areaCount() or perimeterCount(), but we can easily add more in the future. All of the places that used to call checkGameBoard() now need to pass areaCount as the last argument and the default metric to use, and we'll be adding a new call with perimeterCount as the argument for the max-perimeter algorithm in Solver:

  function Solver() {
    // ...

    this.maxPerimeter = function() {
      var max_control = _.max(controls, function(control) {
        return control.checkGameBoard(1, perimeterCount);
      });
      this.index = max_control.index;
    }
  }

This is the beauty of functional programming. We're just passing around the function that we want to use for a certain action, and it ends up being wonderfully clean, elegant, and flexible. This algorithm we just created happens to have the exact same structure as the greedy algorithm, so we can actually modify the Solver.greedy() function to accommodate both metrics at once:

    this.greedy = function() {
      var max_control = _.max(controls, function(control) {
        return control.checkGameBoard(1, that.metric);
      });
      this.index = max_control.index;
    }

And then we set the metric used in this algorithm in the switch statement that selects the algorithm to run, along with adding in the new case for the max-perimeter algorithm:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'greedy':
            that.solverType = that.greedy;
            that.metric = areaCount;
            break;
          case 'greedy-look-ahead':
            that.solverType = that.greedyLookAhead;
            that.metric = areaCount;
            break;
          case 'max-perimeter':
            that.solverType = that.greedy;
            that.metric = perimeterCount;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

With the new algorithm added, we just need to add max-perimeter to the list of algorithms in the UI, and we can test it out:

Surprisingly, this new heuristic outperforms the base area-counting heuristic for the greedy algorithm. It also has some interesting behavior that can be seen while it's running. Quite often it will make choices in moves that end up leaving one block color on the board for an extended set of moves while it clears away the other colors:

This delayed clearing of one color may help explain why this metric does better than area-counting with no look-ahead, because one color choice is saved while the others are being cleared, and a few moves of that saved color can be combined into one color-clearing move. This strategy works well enough that it's worth about as much as looking one more move ahead, as can be seen when stacking up the results with the other algorithms:

Algorithm	Min	Mean	Max	Stdev
RR with Skipping	37	46.9	59	4.1
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
Greedy Look-Ahead-2	28	37.0	45	3.1
Greedy Look-Ahead-3	25	34.2	40	2.7
Greedy Look-Ahead-4	25	33.3	39	2.6
Greedy Look-Ahead-5	25	33.1	41	2.8
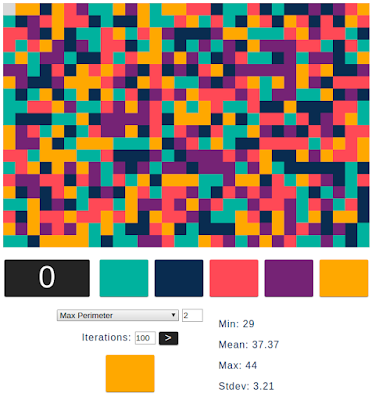
Max Perimeter	29	37.4	44	3.2

This just goes to show that it's worthwhile to try out different things and see how they work. I wasn't expecting a different heuristic to make much of a difference here, but max-perimeter was actually significant. It should be interesting to see what happens when we extend the max-perimeter heuristic to look-ahead, which is now quite easy to do.

Max Perimeter Look-Ahead

Since the max-perimeter algorithm is a heuristic that already works with the greedy algorithm, all we have to do to get it working with the greedy look-ahead algorithm is modify Solver.greedyLookAhead() to use the metric that's being set in the switch statement:

    this.greedyLookAhead = function() {
      var max_control = _.max(controls, function(control) {
        if (control.checkGameBoard(1, that.metric) === 0) {
          return 0;
        }
        return greedyLookAheadN(2);
      });
      this.index = max_control.index;
    }

And we make the same change in greedyLookAheadN(), since that function also calls Control.checkGameBoard():

    function greedyLookAheadN(move) {
      return _.max(_.map(controls, function(control) {
        var matches = control.checkGameBoard(move, that.metric);
        if (matches === 0 || move >= max_moves) {
          return matches;
        }
        return greedyLookAheadN(move + 1);
      }));
    }

Finally, we can add the max-perimeter look-ahead algorithm to the switch statement and to the UI algorithm list:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'max-perimeter':
            that.solverType = that.greedy;
            that.metric = perimeterCount;
            break;
          case 'max-perimeter-look-ahead':
            that.solverType = that.greedyLookAhead;
            that.metric = perimeterCount;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

And voila, we already have another algorithm that we can evaluate for multiple levels of look-ahead. After running up to look-ahead-by-5, the following table shows how the max-perimeter look-ahead algorithm compares to the original greedy algorithm:

Algorithm	Min	Mean	Max	Stdev
RR with Skipping	37	46.9	59	4.1
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
Greedy Look-Ahead-2	28	37.0	45	3.1
Greedy Look-Ahead-3	25	34.2	40	2.7
Greedy Look-Ahead-4	25	33.3	39	2.6
Greedy Look-Ahead-5	25	33.1	41	2.8
Max Perimeter	29	37.4	44	3.2
Max Perimeter Look-Ahead-2	27	35.0	44	2.8
Max Perimeter Look-Ahead-3	27	35.0	41	2.9
Max Perimeter Look-Ahead-4	26	34.8	43	3.3
Max Perimeter Look-Ahead-5	28	34.9	46	2.9

The look-ahead-by-2 run looks better than the corresponding greedy look-ahead-by-2 run with area-counting, but beyond that, the max-perimeter heuristic seems to hit a wall of diminishing returns, and it can never quite get as good as the later greedy area-counting runs. This is useful information, and there may be a reasonable explanation for this lagging performance.

The max-perimeter heuristic seems to be more efficient, reaching better performance without looking as far ahead, but it seems to suffer near the end of the game. At the end of the game, when the board is mostly cleared and there are only a few colored blocks left, there won't be much of any new perimeter made with any given move choice. It's more important to increase the perimeter rapidly early in the game, and later in the game we want to finish off with removing as many blocks as possible on each move. This strategy calls for a hybrid approach, where we use the max-perimeter heuristic for the first, oh 20 moves, let's say, and then switch to the area-counting heuristic to finish it off. We can easily make such a heuristic to explore this hypothesis:

  function perimeterAreaHybrid() {
    if (moves >= 20) return areaCount();
    return perimeterCount();
  }

And we add this hybrid heuristic to the list of choices:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'perimeter-area':
            that.solverType = that.greedy;
            that.metric = perimeterAreaHybrid;
            break;
          case 'perimeter-area-look-ahead':
            that.solverType = that.greedyLookAhead;
            that.metric = perimeterAreaHybrid;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

Now we can run it and see how it compares to the other algorithms:

Algorithm	Min	Mean	Max	Stdev
RR with Skipping	37	46.9	59	4.1
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
Greedy Look-Ahead-2	28	37.0	45	3.1
Greedy Look-Ahead-3	25	34.2	40	2.7
Greedy Look-Ahead-4	25	33.3	39	2.6
Greedy Look-Ahead-5	25	33.1	41	2.8
Max Perimeter	29	37.4	44	3.2
Max Perimeter Look-Ahead-2	27	35.0	44	2.8
Perimeter-Area Hybrid	31	39.0	49	3.8
Perim-Area Hybrid Look-Ahead-2	27	35.2	43	3.2
Perim-Area Hybrid Look-Ahead-3	27	33.5	41	2.7
Perim-Area Hybrid Look-Ahead-4	26	33.2	41	3.1
Perim-Area Hybrid Look-Ahead-5	28	33.0	41	2.5

Again, I'm surprised at how this algorithm performs, but this time it doesn't work as well as I thought it would. It does seem to perform a bit better than the max-perimeter look-ahead-by-2 version once it gets to look-ahead-by-3, but I was expecting it to do better than the greedy look-ahead-by-3 and later versions and it never quite achieves that. Maybe the hybrid approach doesn't work as well as I'd hoped, or we're just reaching the natural limits of what an algorithm can do in this game. Let's explore another avenue.

Constructing a Deep-Path Algorithm

The idea of clearing a deep path of blocks into the game board before expanding outward is another strategy that has some potential to work well. In manual attempts at playing the game, I found that this strategy of making a path deep into the center of the board first generally worked pretty well for clearing the board in a lower number of moves, and I could easily get below 35 moves when I drove towards the middle of the board first.

We should be able to encompass this strategy in another heuristic to use with the greedy algorithm, and it seems somewhat similar to maximizing perimeter. We can accentuate that type of search by trying to maximize the perimeter-area ratio, which should give added weight to color choices that result in long, narrow paths into the board. The corresponding metric function is straightforward:

  function ratioCalc() {
    var area = areaCount();
    if (area === 0) return area;
    return perimeterCount() / area;
  }

Here we are careful to not divide by zero, and we can add a couple more algorithms to the list of choices:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'deep-path':
            that.solverType = that.greedy;
            that.metric = ratioCalc;
            break;
          case 'deep-path-look-ahead':
            that.solverType = that.greedyLookAhead;
            that.metric = ratioCalc;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

This heuristic is fascinating because it does pretty much exactly what I wanted it to do. Take a look at an example game in progress:

Deep, narrow paths are made into the blocks, as desired, but the algorithm performs terribly. Take a look at some runs with different look-aheads compared to the other algorithms:

Algorithm	Min	Mean	Max	Stdev
RR with Skipping	37	46.9	59	4.1
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
Greedy Look-Ahead-2	28	37.0	45	3.1
Greedy Look-Ahead-3	25	34.2	40	2.7
Max Perimeter	29	37.4	44	3.2
Max Perimeter Look-Ahead-2	27	35.0	44	2.8
Perimeter-Area Hybrid	31	39.0	49	3.8
Deep-Path	51	74.8	104	9.4
Deep-Path Look-Ahead-2	50	74.9	112	9.8
Deep-Path Look-Ahead-3	50	75.2	112	9.8
Deep-Path Look-Ahead-4	50	75.4	112	9.5

It doesn't even improve as it looks further and further ahead. The problem is likely that while it may be a good idea to create a deep path at the beginning of the game, it's a waste of moves to keep doing it on the 30th move, and definitely has run its course by the 70th move. It may be worth seeing if using this heuristic only in the beginning will improve things with a hybrid heuristic similar to the perimeter-area hybrid approach we tried before. We can make a simple heuristic to try out this theory:

  function ratioAreaHybrid() {
    if (moves >= 12) return areaCount();
    return ratioCalc();
  }

I picked a move threshold of 12 simply by looking at where the deep path generally stops usefully extending when clicking through a game manually using the deep-path heuristic. We can also add a couple more choices to the list of algorithms:

      $('#solver_type').change(function () {
        switch (this.value) {
          // ...
          case 'path-area':
            that.solverType = that.greedy;
            that.metric = ratioAreaHybrid;
            break;
          case 'path-area-look-ahead':
            that.solverType = that.greedyLookAhead;
            that.metric = ratioAreaHybrid;
            break;
          default:
            that.solverType = that.roundRobin;
            break;
        }

This version of the algorithm performs much better than the pure deep-path version, but it never quite achieves the performance of the original greedy algorithm or even the max-perimeter heuristic:

Algorithm	Min	Mean	Max	Stdev
RR with Skipping	37	46.9	59	4.1
Random with Skipping	43	53.1	64	4.5
Greedy	31	39.8	48	3.5
Greedy Look-Ahead-2	28	37.0	45	3.1
Greedy Look-Ahead-3	25	34.2	40	2.7
Max Perimeter	29	37.4	44	3.2
Max Perimeter Look-Ahead-2	27	35.0	44	2.8
Perimeter-Area Hybrid	31	39.0	49	3.8
Deep-Path	51	74.8	104	9.4
Path-Area Hybrid	35	44.2	54	3.5
Path-Area Hybrid Look-Ahead-2	34	40.8	49	3.0
Path-Area Hybrid Look-Ahead-3	31	39.0	47	3.2
Path-Area Hybrid Look-Ahead-4	32	38.7	45	2.7

Even though it seemed like a good idea to start with a deep path toward the center of the board before spreading out and clearing more blocks, it just doesn't make progress fast enough to overcome the initial slowness of creating that deep path at the start. Oh well, it was worth a try, at least.

We've covered a lot of ground in this exploration of other heuristics for the greedy algorithm, and we've learned a lot about what makes a good heuristic. While we found some promising options by attempting to maximize the perimeter or take a hybrid approach of combining different heuristics, it turns out that it's fairly difficult to do better than the basic greedy algorithm of clearing out the most blocks on the current move or, even better, looking ahead to see how to clear out the most blocks a few moves ahead.

Even though we didn't find a better heuristic, it's still worth exploring because we improved the flexibility of the code and made it easier to add in more heuristics in case we come up with other ideas for potentially better ones in the future. We now have a ton of knobs and dials to fiddle with, and it's possible to spend an awful lot of time tweaking and tuning things. It also cannot be overstated how important and useful it is to gain as much knowledge about a problem space as possible. You never know when you'll come across a key insight that leads to a solution with much better performance. Next time we'll put additional heuristics for the greedy algorithm aside and instead turn to exploring other types of standard graph search algorithms. There are plenty of other algorithms to try, and we can see if it's possible to use them to some extent with the harsh exponential growth of move choices with this game.


Article Index
Part 1: Introduction & Setup
Part 2: Tooling & Round-Robin
Part 3: Random & Skipping
Part 4: The Greedy Algorithm
Part 5: Greedy Look Ahead
Part 6: Heuristics & Hybrids
Part 7: Breadth-First Search
Part 8: Depth-First Search
Part 9: Dijkstra's Algorithm
Part 10: Dijkstra's Hybrids
Part 11: Priority Queues
Part 12: Summary